Here we are going to implement the Linear Regression in python. Since the code was already explained in previous regression posts, here explanation will be given wherever necessary.
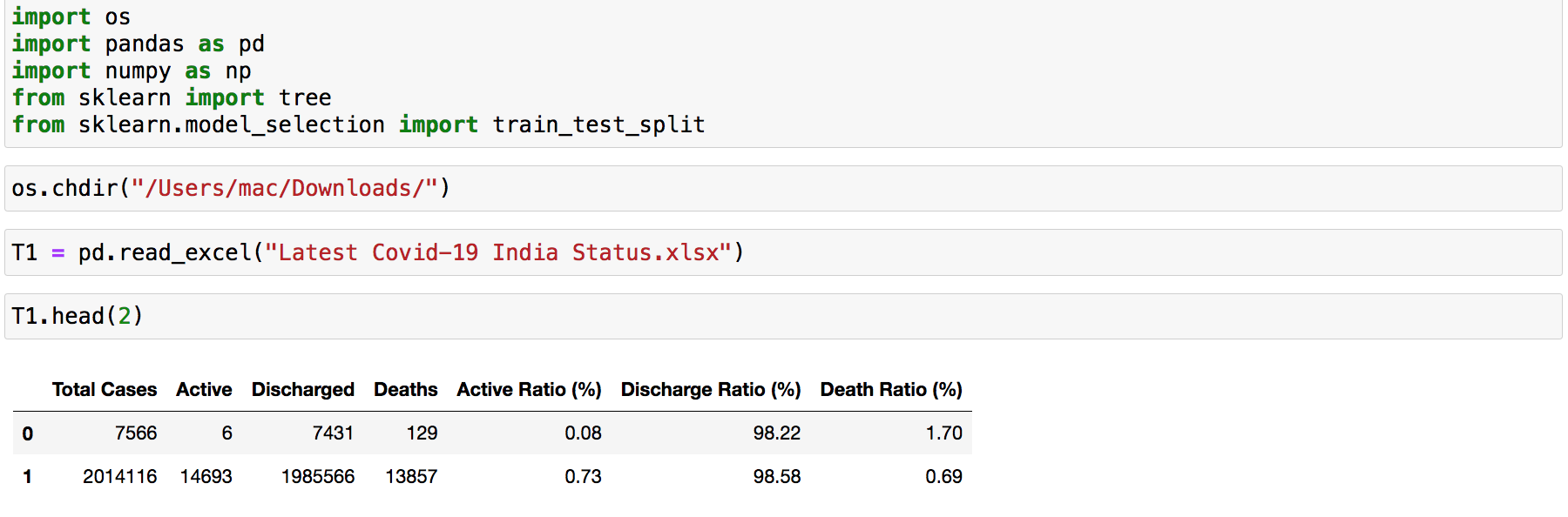
Load the libraries, set the path and Load Data
import os
import pandas as pd
import numpy as np
from sklearn import tree
from sklearn.model_selection import train_test_split
os.chdir(“/Users/mac/Downloads/”)
T1 = pd.read_excel(“Latest Covid-19 India Status.xlsx”)
Train, Test Split, and Building Model
train, test = train_test_split(T1, test_size=0.2)
import statsmodels.api as sm
Model = sm.OLS(train.iloc[:,6],train.iloc[:,0:6]).fit() 
Model Summary is below
Model.summary()
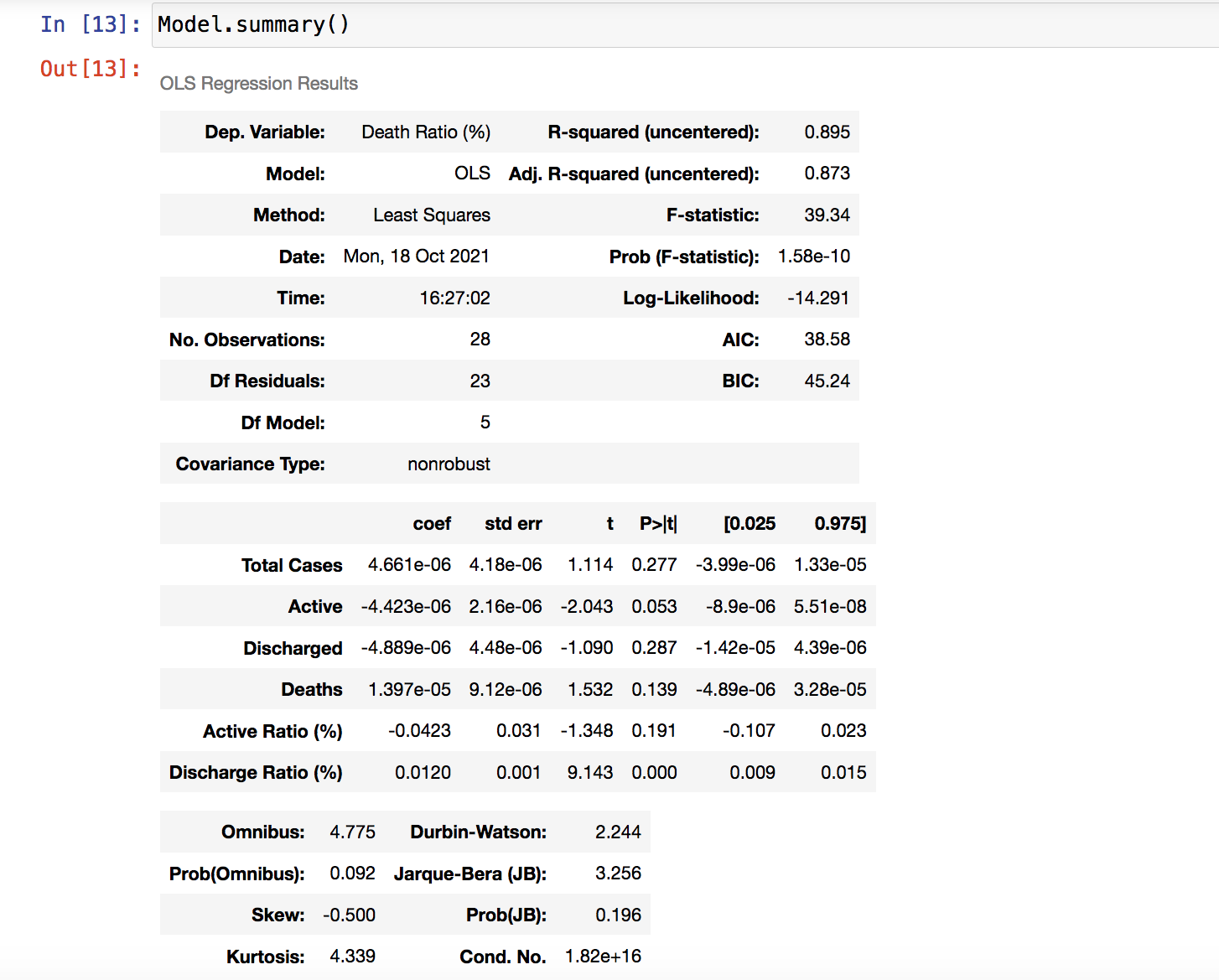
In Above Picture
- Dep Variable is a Dependent Variable.
- Model is OLS- Ordinary Least Squares
- Method is Least Squares
- Date and Time is mentioned
- No of Observations to build this Model ( Training Data Observation )
- Degress of Freedom ( We already saw in Feature Selection- Categorical)
- Df Model is nothing but nmber of Independent variable in the Model.
- Covariance Type is Non Robust
- R- Squared - It explains the variance percentage of Target Variable explained by the Target Variable.
- Adj R Squared- It can not be greater than R- Squared - It actually increase when we add more useful variables and decrease when we add more useless variables.
- F- Statistic - Represents the difference between actual and predicted values. It should be as low as it can.
- probability - If it is less than 0.05, then the Model is good.
- Log Likelihood - Log of Likelihood function
- AIC- The Akaike Information Criterion (AIC) . It adjusts the Log Likelihood, based on the number of observations and complexity of the Model.
- BIC - Bayesian Information Criterion is for model selection among a finite set of models.
When we build multiple models, and find the same accuracy, then based on the AIC, we will select the Model.
Let us see the second table in above picture.
- First column is coefficient and it tells how much information is explained by the variable in the row. It should be interpreted as 1 unit increase in the independent variable will lead to mentioned coefficient % times increase in the Target Variable.
- In the Linear Regression formula, b1, b2 will be taken from this coefficient column.
- Std - err- Basic Standard Deviation
- T value- It measures how statistically signicant the coefficient is.
P> t -Based on T value, we calculate P value. If P value is less than 0.05 then we say that particular variable is important. - Since P is calculated using t value, t will drive whether to select or reject the variable for the Model.
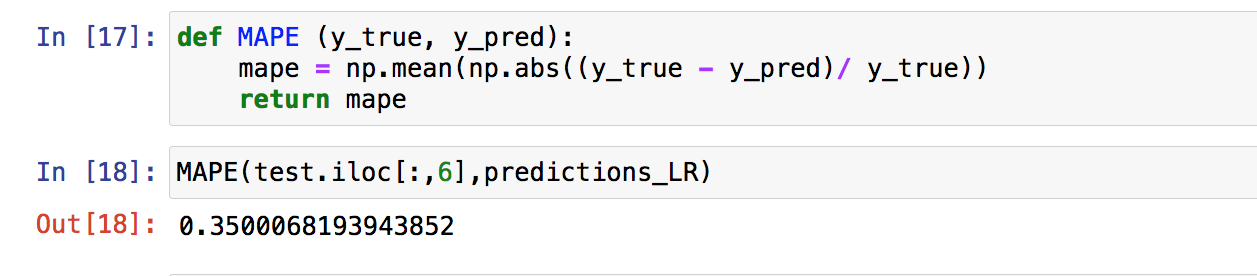
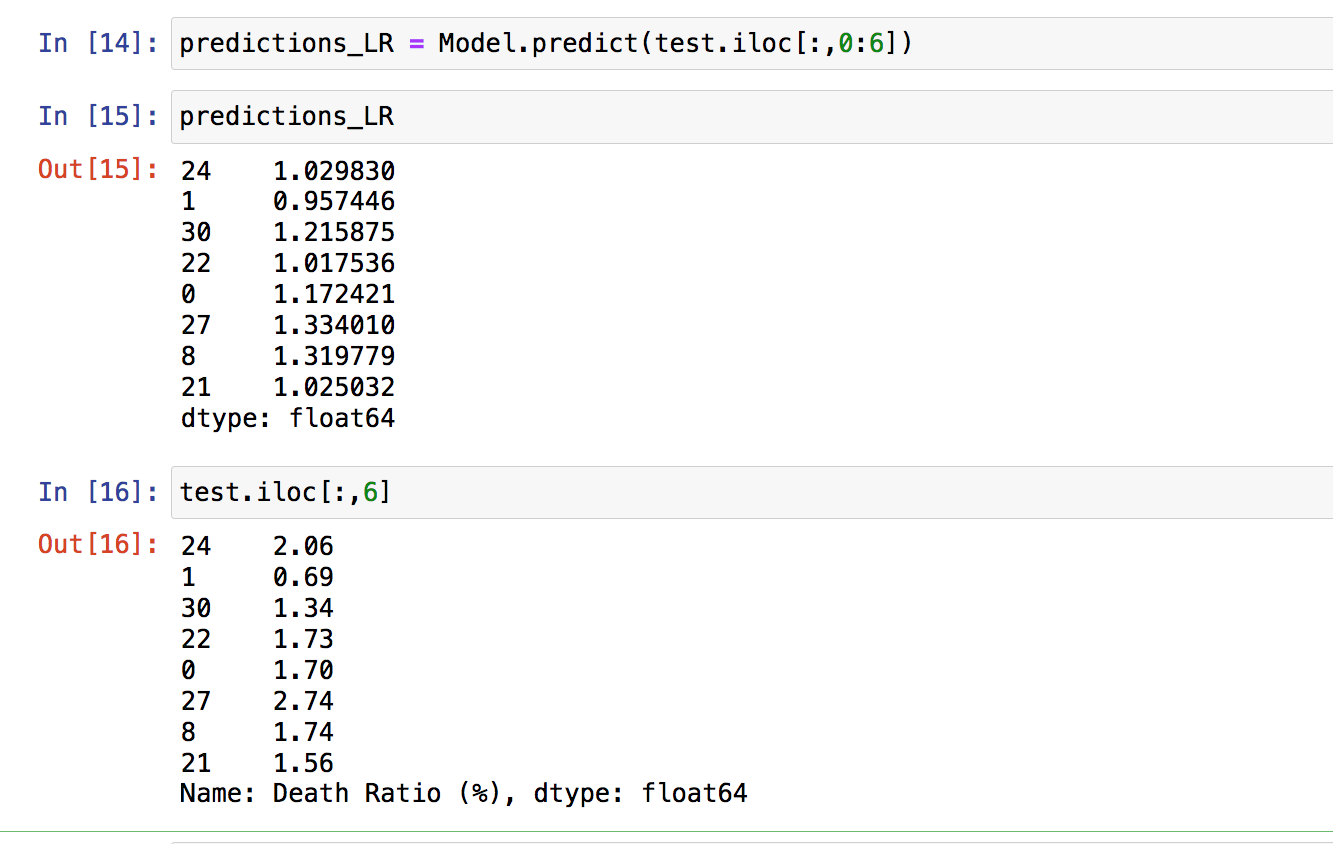
Prediction and Actual Values
predictions_LR = Model.predict(test.iloc[:,0:6])
MAPE function to measure accuracy as a percentage of error
def MAPE (y_true, y_pred):
mape = np.mean(np.abs((y_true - y_pred)/ y_true))
return mape
MAPE(test.iloc[:,6],predictions_LR)