Link Search Menu Expand Document

We know ML algorithm create patterns and stores and applies the pattern the test data. In case of statistical model, it calculates coefficient. Coefficient explains the weight of each independent variable and use the weight to develop ML Model for test data calculation.

Statistical Models

Below are some Statistical Models.

  • Linear Regression
  • Logistic Regression
  • Time Series Analysis

    Linear Regression

    Linear Regression is only used for Regression and can only be applied on continuous variable. It can not be used for classification. We can use this for Missing Value Analysis as well. There are two types of Regression.

  • Simple Linear Regression( It is used when we have one independent variable)
  • Multiple Linear Regression( When we have more than one independent variable, we go with this) Besides prediction, it also helps to find the relationship between variables. Linear Regression Equation The Goal of Linear Regression Algorithm is devleop the below equation.

Based on above equation, hypothesis is built and evaluated. H0 : b1 is equal to Zero. Null Hypothesis : b1 is not contributing to Target Variable. H1 : b1 is not equal to Zero. Alternate Hypothesis: b1 is contributing to Target Variable.

Is the P value is less than 0.05, then we reject null hypothesis.

And formula for correlation between two variables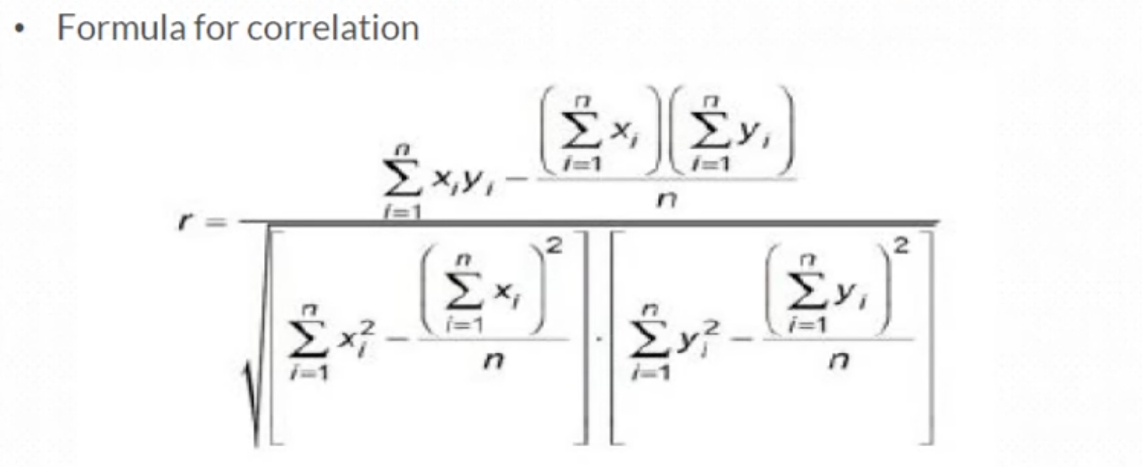

And correlation ranges from -1 to 1. -1 - Negatively correlated.
+1 - Positively correlated. 0 - No relation between variables.

Parameters to evaluate Linear Regression

  • R- Squared
  • Adjusted R-Square

Above Methods, evaluate training data as well.

R-Squared

R Squared is the proportion of variance in the dependent variable which can be explained by the independent variables. Example R Squared is 0.86, then 86% of Target Variable is explained by all the independent variables. Below is the formula for R-Squared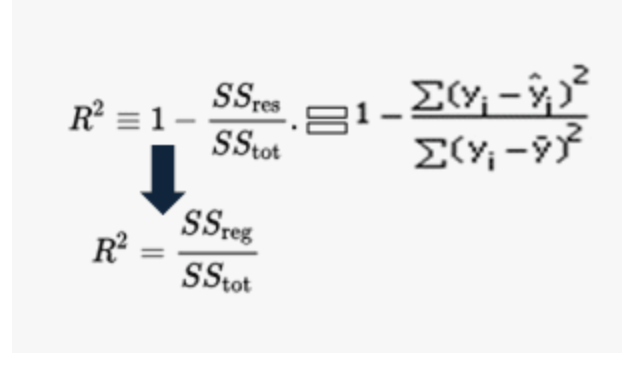

Adjusted R-Squared

Every time you add a independent variable to a model, the R-squared increases, even if the independent variable is insignificant. It never declines. Whereas Adjusted R-squared increases only when independent variable is significant and affects dependent variable.

If the particular variable is not carrying much information, then p value will decide whether to accept the variable.(Accept the Null Hypothesis or Reject Null hypothesis)

Pre Requisite to Linear Regression

  • Linear Relationship :- The Data that is fed to the Model, will have the linear relationship between dependent and independent variable. Either it is positively correlated or negatively correlated.
  • Normality:- The data that is being fed to the Model, should be normally distributed.(We can look for historgrams to check for whether data is normally distributed.)
  • Muticollinearity :- If two variables are highly correlated, then we need to feed only one variable to the Model.
  • Auto Correlation:- There should be no correlation between error. Which means errors are independent, it should not follow any patterns.

If the dataset satisfies above pre requisites then we can go ahead and build Linear Regression Model. Through the equation we can find the Target value for the test data.